加重移動平均と指数平滑移動平均

   移動平均の基本となる単純移動平均（Simple Moving Average：SMA）は、計算がシンプルで分かりやすい点も広く普及している要因の一つですが、次のような問題点を指摘する人がいます。

• Ａ：新しい情報（レート）は古い情報よりも重要であるはずだが、単純移動平均ではみな同等に扱われている。つまり、計算期間における単純な平均値に過ぎない。
• Ｂ：単純移動平均では、計算期間の情報しか反映されていない。それよりも古い情報は切り捨てられ無視 されている。

   Ａについてはなんとなく納得できると思いますが、Ｂでは何が問題なのか、補足説明が必要かもしれません。例えば10日移動平均は本日から９日前までのレートで計算し、10日前のレートは計算の対象外です。もし10目前に非常に大きな動きがあった場合、本日の移動平均と昨日の移動平均では値にギャップが生じます。本来スムーズである移動平均にそこだけ階段のような落差が生まれてしまうのです。それはそれで受けいれるのも一つですが、解決策を考えた人もいます。そうしたことから、移動平均にはいくつかのバリエーションが存在します。以下では、加重移動平均と指数平滑移動平均についてご説明します。

   加重移動平均（Weighted Moving Average：WMA）は前述の問題点Ａに対処したバリエーションです。単純移動平均では、本日の終値も○日前の終値も同等の重みを持っています。しかし、情報は新しいほうがより重要であるという考え方もあります。そこで、要素が新しければ新しいほど段階的に計算結果への影響度が増すように工夫したのが加重移動平均です。例えば3日移動平均の場合は次のように計算します。

• 単純移動平均…（本日の終値＋昨日の終値＋一昨日の終値）÷3
• 加重移動平均…（（本日の終値×3）＋（昨日の終値×2）＋（一昨日の終値×1））÷6

   これによって、本日の終値は一昨日の終値よりも3倍の重みを持つことになります。10日であれば、【（（本日の終値×10）＋（昨日の終値×9）…＋（9日前の終値×1））÷55】という計算になります。では具体的に10日の単純移動平均と加重移動平均を比べて見てみましょう。

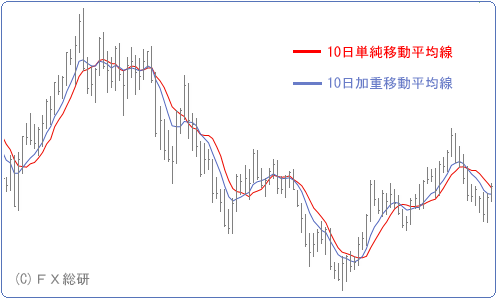
   加重移動平均は直近のレートにより強く影響を受けますので、単純移動平均に比べて動きが早くなっていることが見てとれると思います。

   加重移動平均は情報の重みに差を設けましたが、計算期間が限定されるという点では単純移動平均と同じです。指数平滑移動平均（Exponential Moving Average：EMA）は、両方の問題に対処したバリエーションです。具体的な計算式は以下のとおりです。

• 指数平滑移動平均＝（本日の終値−前日の指数平滑移動平均）×α＋前日の指数平滑移動平均

   αは平滑化係数と呼ばれるパラメータで、本日の終値の重みをどの程度にするかを決めるものです。0＜α＜1の値で、0．1よりも0．9のほうが加重は大きくなります。しかし計算式だけでは何のことだかピンときませんね。要するに、指数平滑移動平均のポイントは次の二つです。

• 本日の終値を加重している。
• 計算期間に関係なく限りなく古い情報も引き継がれる。

   この結果どうなるか。加重の仕方の違いを加重移動平均と指数平滑移動平均で比べてみましょう。

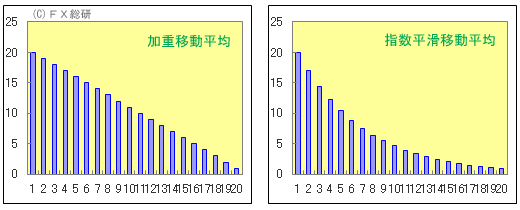
   図のような感じで、指数平滑移動平均では遠い過去の値も寄与度は決してゼロにはなりません。ここが加重移動平均と異なる点です。なお、指数平滑移動平均の計算には常に前日の値が必要となります。すると最初の日は算出できないことになり、さらに二日目をどうするかという疑問が残ります。これにはいくつかの方法がありますが、通常は単純に前日の終値を採用します。

   加重移動平均や指数平滑移動平均も、テクニカル分析としての使用方法は基本的に単純移動平均と同じですので、「移動平均」をご参照ください。最後に、単純移動平均、加重移動平均、指数平滑移動平均を一つのチャートにプロットしてみましたので、比べてみてください。

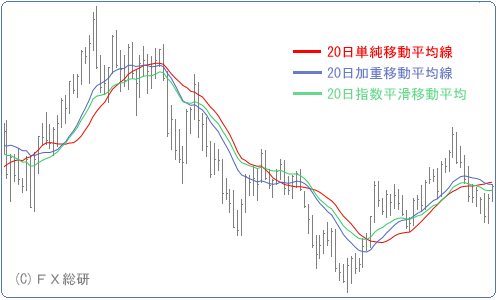
   加重移動平均や指数平滑移動平均は、実戦ではさほど用いられていないようです。その理由は、単純移動平均と比べて格別に精度が高いという印象がないからでしょう。事実、ある米国の証券会社がテストしたところではそうした結果も出ているとのこと。早い話しが一長一短なのです。ただ、補助的な分析手法として有効ですし、指数平滑移動平均は後で取り上げるＭＡＣＤにも応用されています。知っておいて損はありません。